必修一数学 - 随堂练
第五章:三角函数
一、任意角和弧度制
1. 任意角
题目一
以下各角中,与 2023° 角终边相同的是
A. -223° B. 223° C. -147° D. 147°
解题思路
首先,我们需要将 2023° 化简到 0° 到 360° 之间。使用公式:
计算得:
取整数部分,得到 5。然后计算余数:
所以,正确答案是选项 B。
题目二
以下说法正确的是
A. 小于
C. 终边重合的角一定相等 D. 全不正确
解题思路
答案选 D。
题目三
时针经过四个小时,转过了
解题思路
时钟的时针每小时转过的角度是
因此,时针经过四个小时,转过的角度是:
所以,时针经过四个小时,转过了
题目四
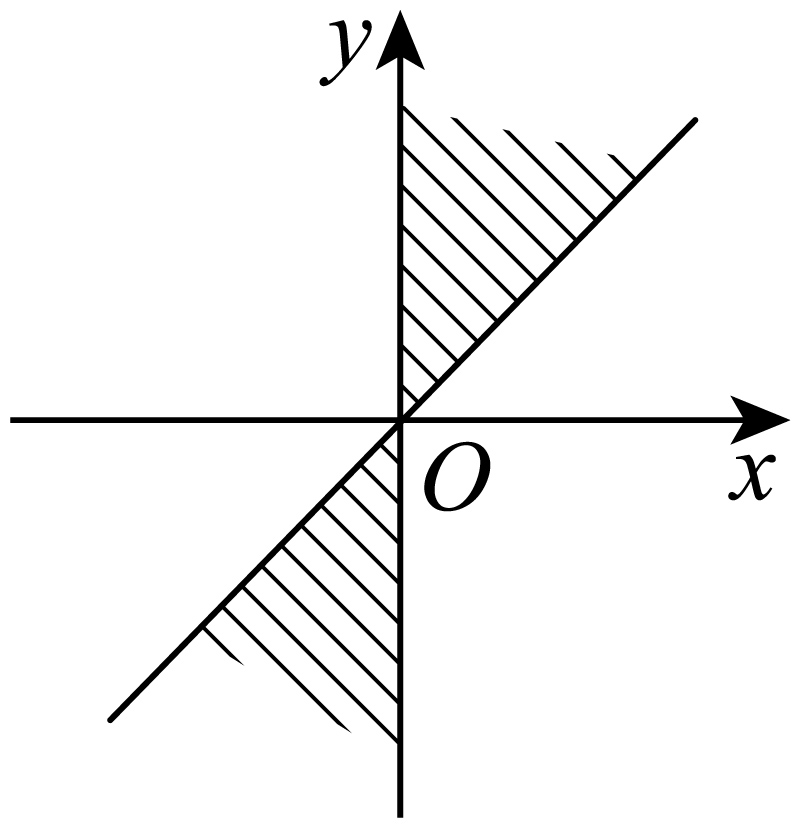
如图所示的图形,那么终边落在阴影部分的角的集合如何表示?
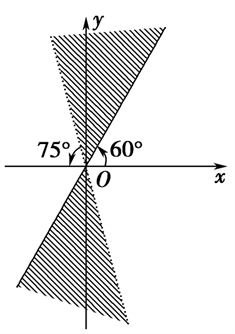
解题思路
取值集合为 { β | k·180°+60° ≤ β < k·180°+105°, k∈Z }
题目五
已知角
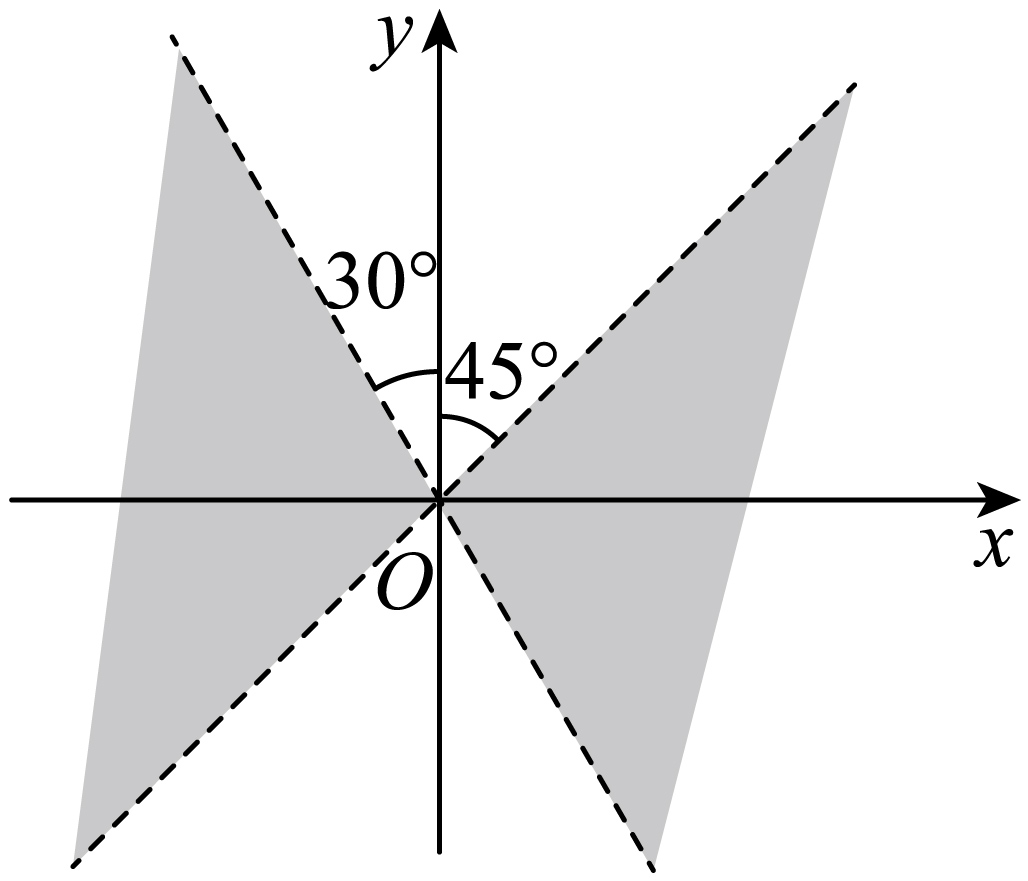
解题思路
答案
其中
2. 弧度制
题目一
弧度制换角度制:
角度制换弧度制:
解题思路
弧度制换角度制
我们知道,
弧度 = 弧度 = 弧度 =
角度制换弧度制
要将角度转换为弧度,我们用角度乘以
= 弧度 = 弧度 = 弧度
题目二
与角
解题思路
用弧度表示为:
题目三
若角
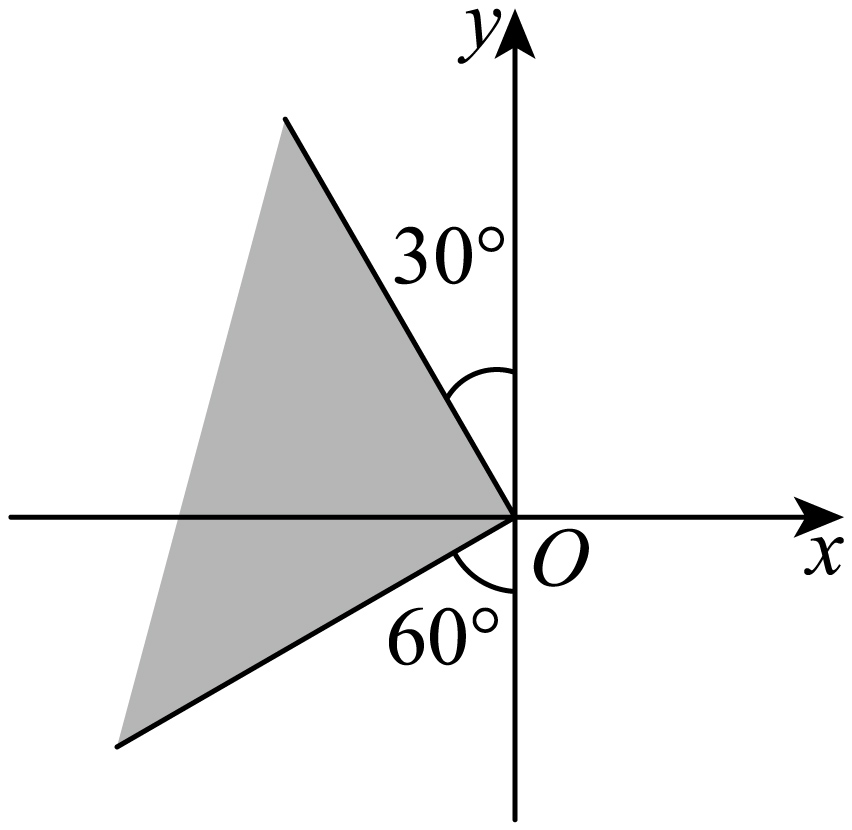
A.
B.
C.
D.
解题思路
【分析】根据给定图形,求出在
【详解】依题意,在
故选:D
题目四
集合
解题思路
题目五
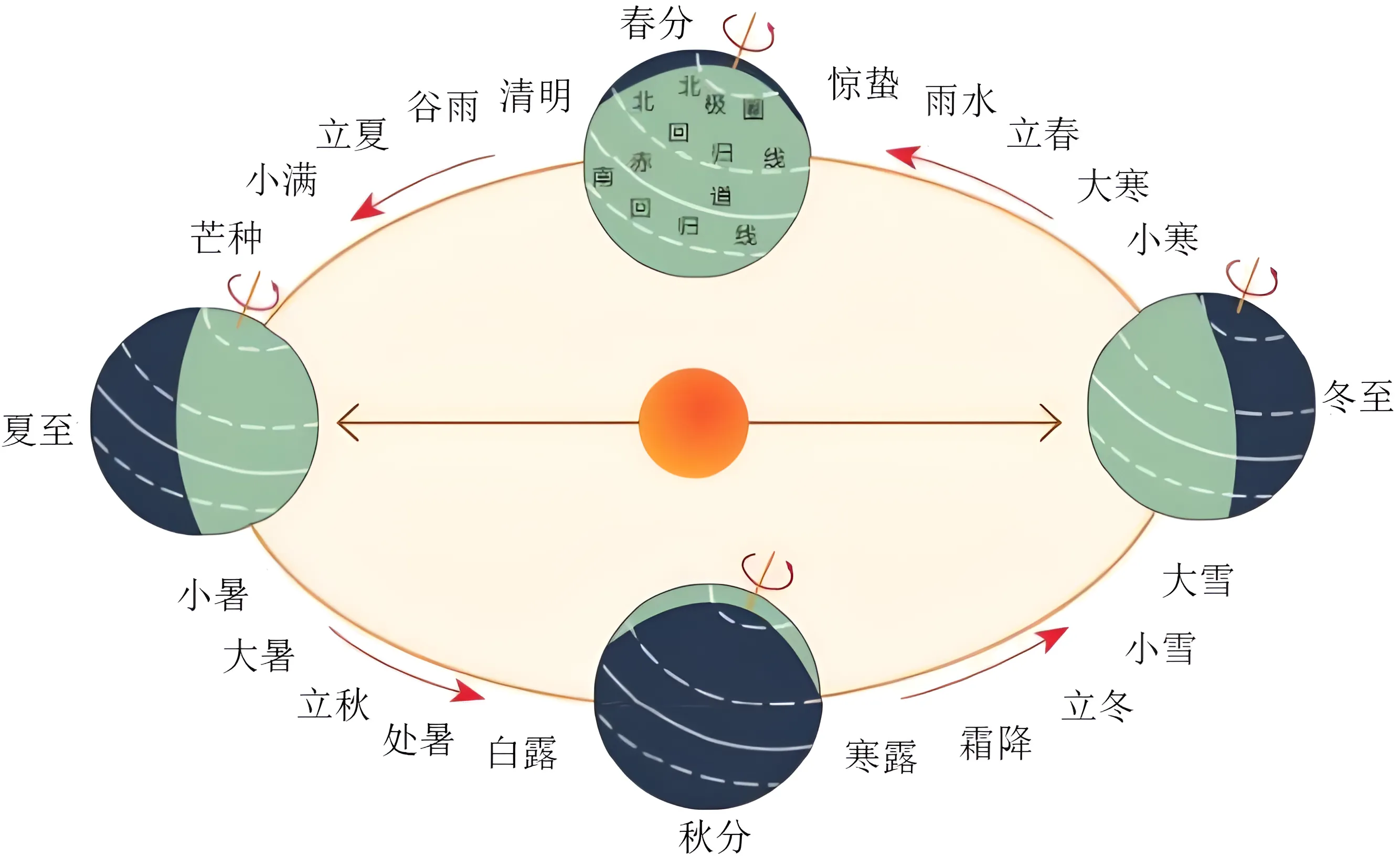
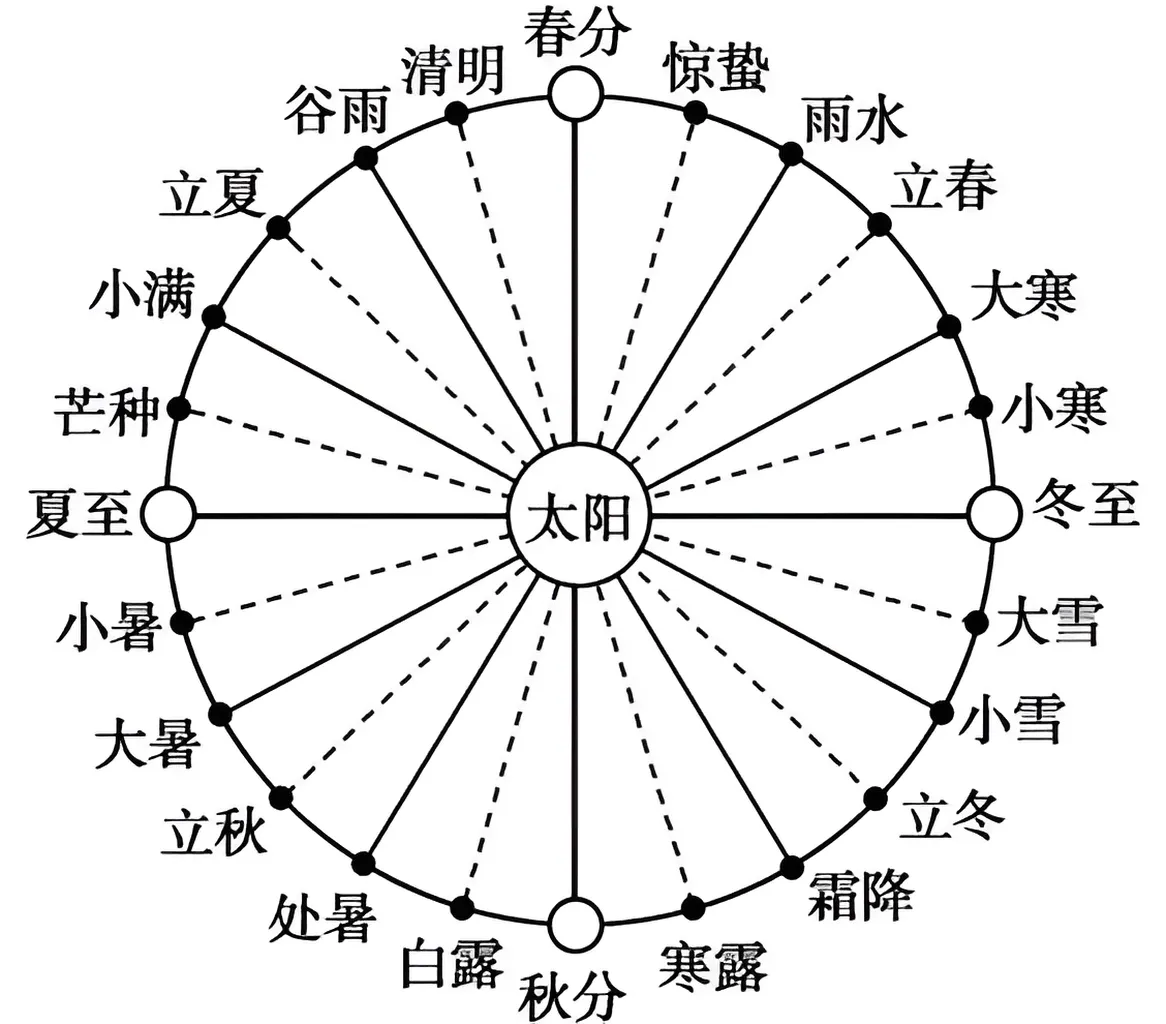
英国浪漫主义诗人 Shelley(雪莱)在《西风颂》结尾写道 “If Winter comes, can Spring be far behind?” 春秋战国时期,为指导农耕,我国诞生了表示季节变迁的 24 节气,它将黄道(地球绕太阳按逆时针方向公转的轨道,可近似地看作圆)分为24等份,每等份为一个节气。2024 年 12 月 21 日为冬至,经过小寒和大寒后,便是立春。则从冬至到次年立春,地球公转的弧度数约为
A.
解题思路
【分析】找到每一等份的度数,进而可得答案。
【详解】由题可得每一等份为
故答案为:A
3. 弧长与面积
题目一
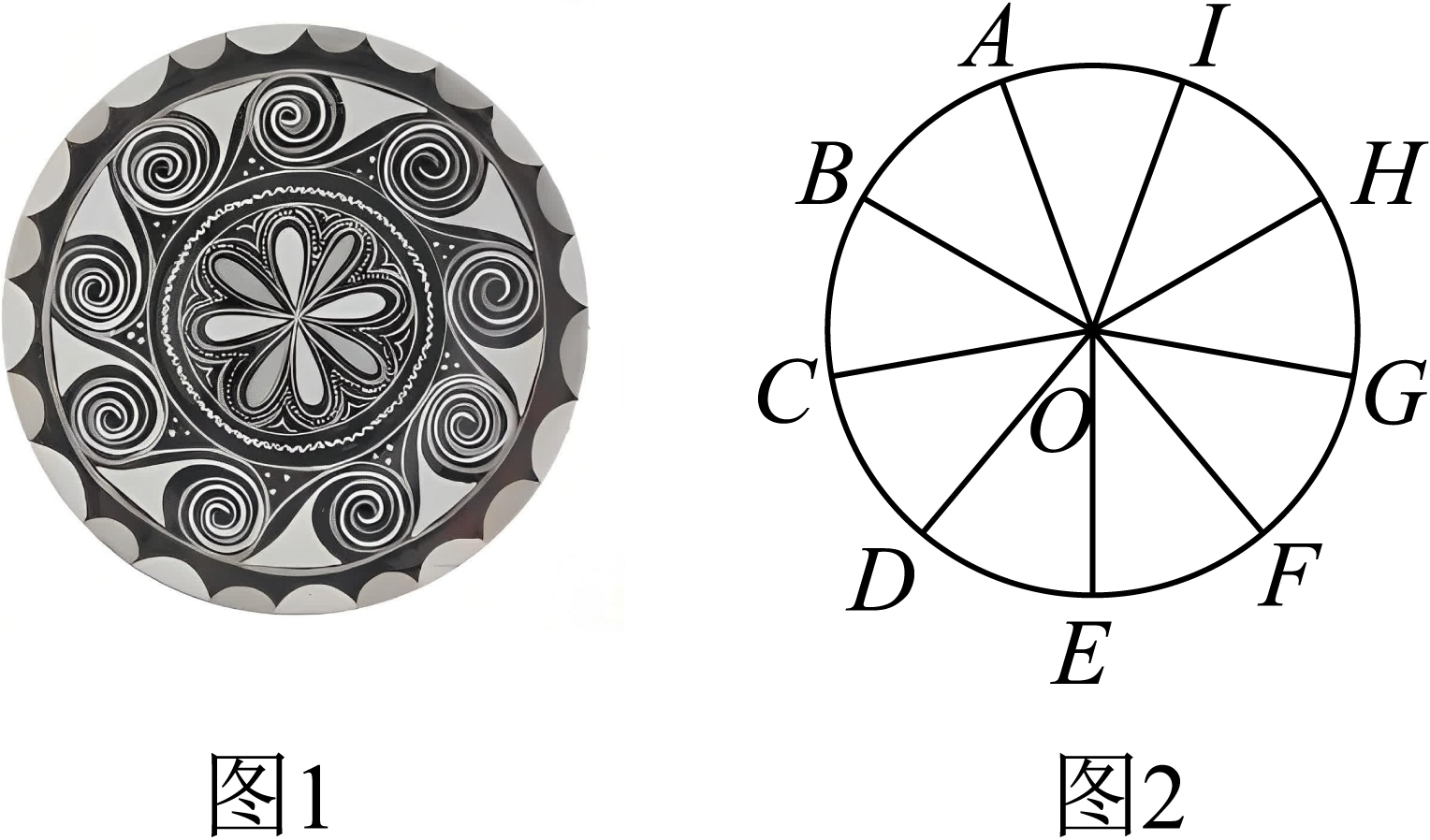
彝族图案作为人类社会发展的一种物质文化,有着灿烂历史。按照图案的载体大致分为彝族服饰图案,彝族漆器图案,彝族银器图案等,其中蕴含着丰富的数学文化,如图 1:漆器图案中出现的“阿基米德螺线”,该曲线是由一动点沿一条射线以等角速度转动所形成的轨迹。这些螺线均匀分布,将其简化抽象为图 2 所示,若 OA 长为 2 个单位,则 ∠AOB 所对应的弧长为
A.
解题思路
根据题意可得,∠AOB 所对的弧长为整个圆的
整个圆周的周长为
所以 ∠AOB 所对应的弧长为
故选:D
题目二
数学中处处存在着美,机械学家莱洛发现的莱洛三角形就给人以对称的美感。莱洛三角形的画法:先画等边三角形
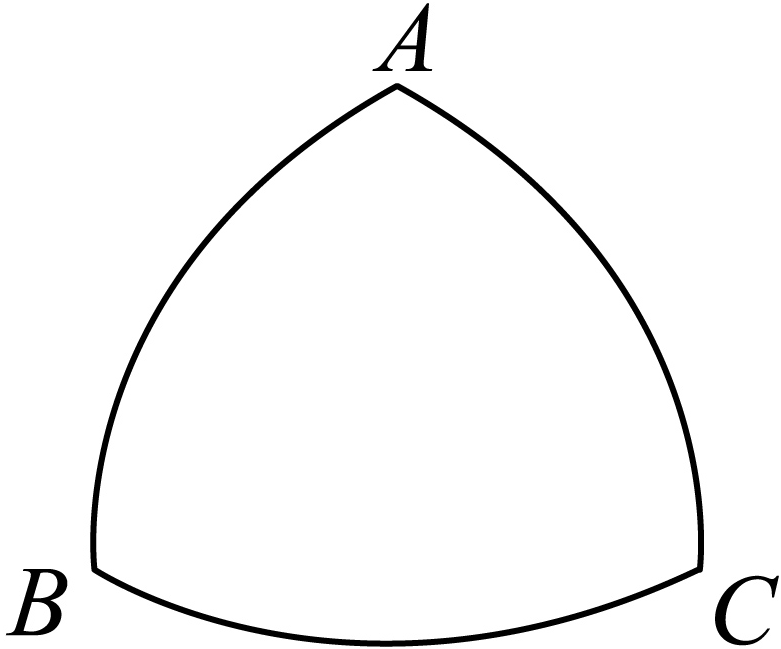
A.
解题思路
由已知得:
设 C 为圆心,则为
故选:D
题目三
如图,正五边形
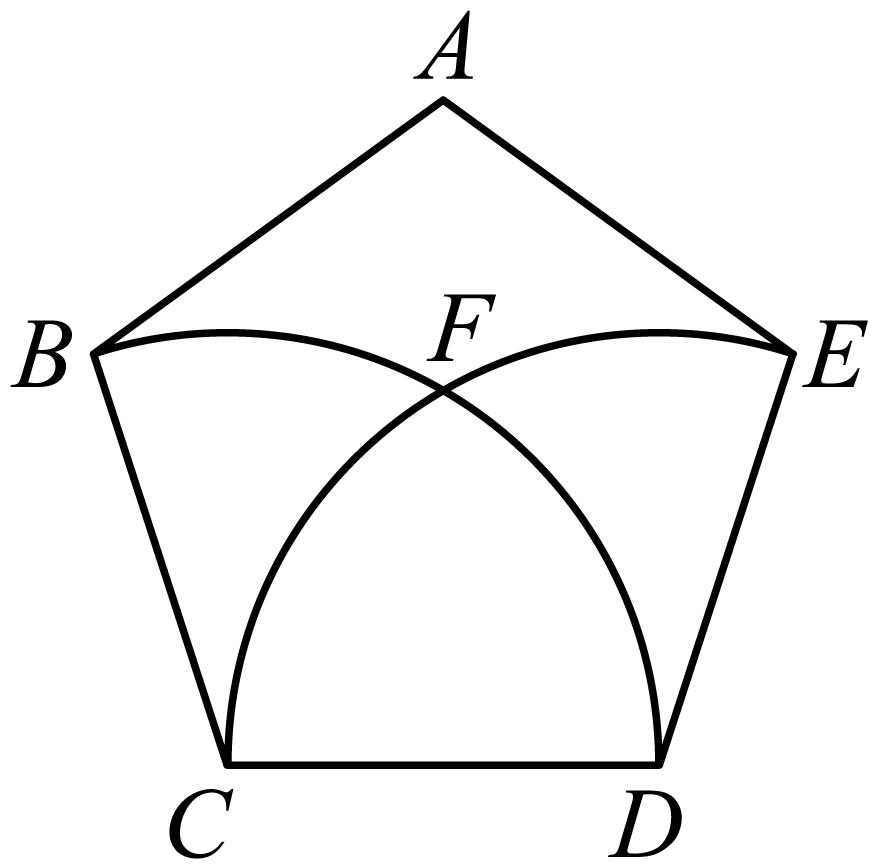
解题思路
思路
连接 CF, DF,得到
解答
连接 CF, DF,则
在正五边形 ABCDE 中,
故答案为:
二、三角函数
1. 任意角的三角函数
1)定义求值
题目一
已知角
A.
解题思路
已知点
因此,
所以,
故答案为:D
题目二
在平面直角坐标系
A.
解题思路
【分析】根据题意利用任意角的三角函数的定义,结合诱导公式可求得结果。
【详解】因为平面直角坐标系
所以
因为
故选:B
2)定义求范围
题目一
若
A.
解题思路
首先,将不等式
在
因此,
故选:D
题目二
在
A.
解题思路
答案为:C
3)同角三角函数间的关系
题目一
已知
若
解题思路
方法:解方程或辅助三角形(推荐)。
答案:
题目二
若
A. 0 B.
解题思路
【分析】 将目标式分子分母同时除以
【详解】
故选:B
【点睛】 本题考查齐次式的化简和求值,属基础题。
题目三
已知
如果
解题思路
已知
如果
2. 诱导公式
1)基本应用
题目一
解题思路
题目二
已知
解题思路
根据诱导公式,
因此,
题目三
已知
A.
解题思路
答案选 D。
2)凑 1
题目一
已知
解题思路
【分析】
观察发现已知和所求都有大量的
【详解】
又因为
(怎样由 ① 求 ②?观察发现 ② 中的
由 ① 可解得
代入 ② 得
3. 三角函数图像与性质
1)基本习题
题目一
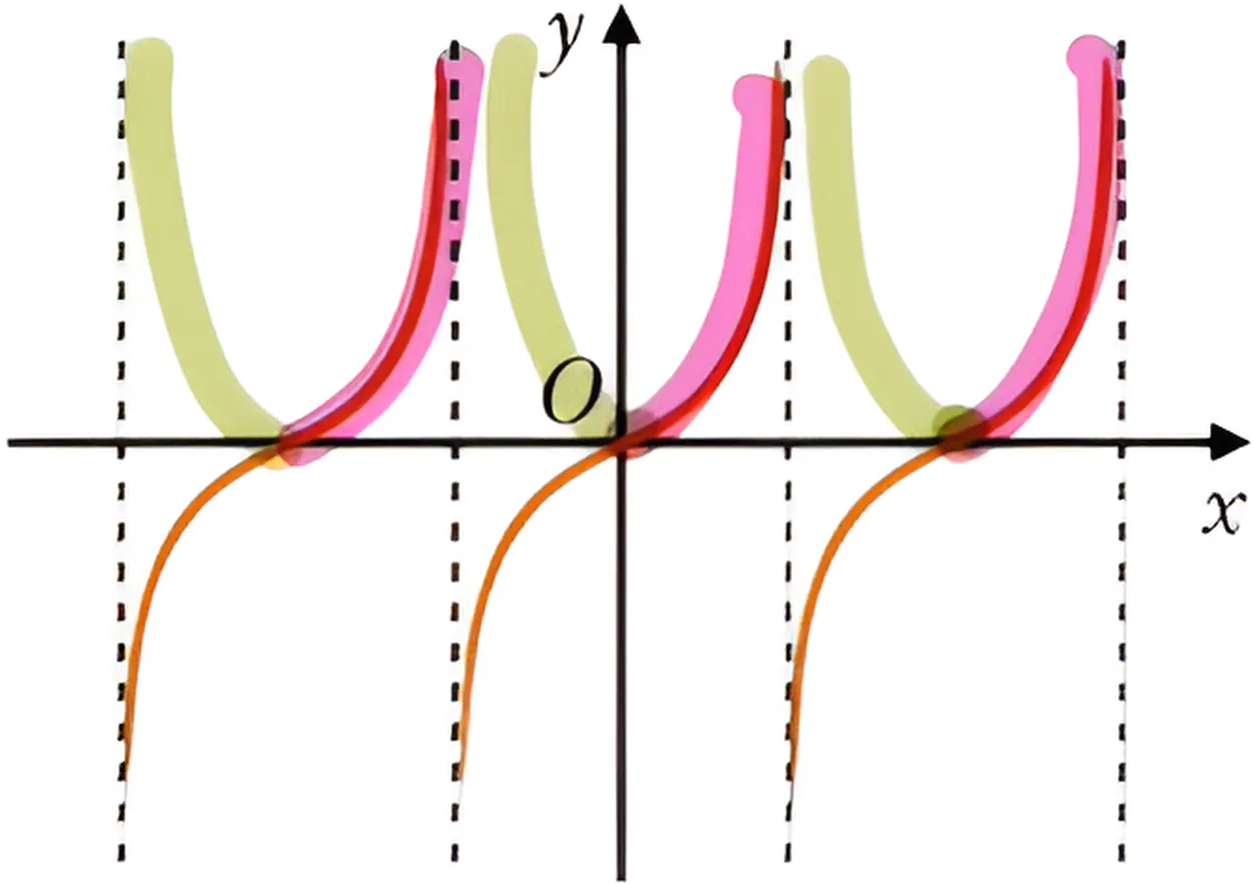
函数
解题思路
答案是
题目二
函数
A.
解题思路
答案是 D。
题目三
不等式
解题思路
不等式
题目四
设常数
A.
解题思路
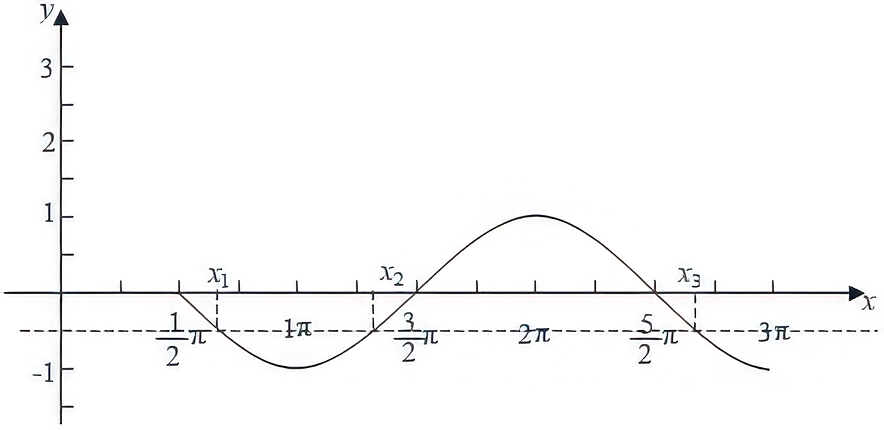
方程
由于
至此,根据下面三个方程,可以解出所有未知数。
把 ①, ② 式子代入 ③ 式,得
(思考一下为什么不求得其他 x 的值?从图中不难看出它们最后的余弦值相等,也就是 m 值相等)
由此,可以根据
故选:B
题目五
已知函数
A.
B.
C.
D. 不等式
解题思路
答案是 B, D。
题目六
函数
A.
B.
C.
D.
解题思路
【分析】由题可知,
答案是 D。
题目七
函数
A.
解题思路
答案是 B。
2)考试题型
题型一:直接画图
已知
解题思路
由于
因此,
所以,
题型二:考复合函数
题目一
函数
解题思路
答案是
题目二
已知函数
解题思路
答案是
4. 做题技巧
1)同角三角函数 - 对偶式
知识点
题目
题目一
[2008 • 浙江高考] 若
A.
解题思路
答案是 B。
题目二
已知
解题思路
答案是
2)巧用三角函数定义
知识点
题目
题目一
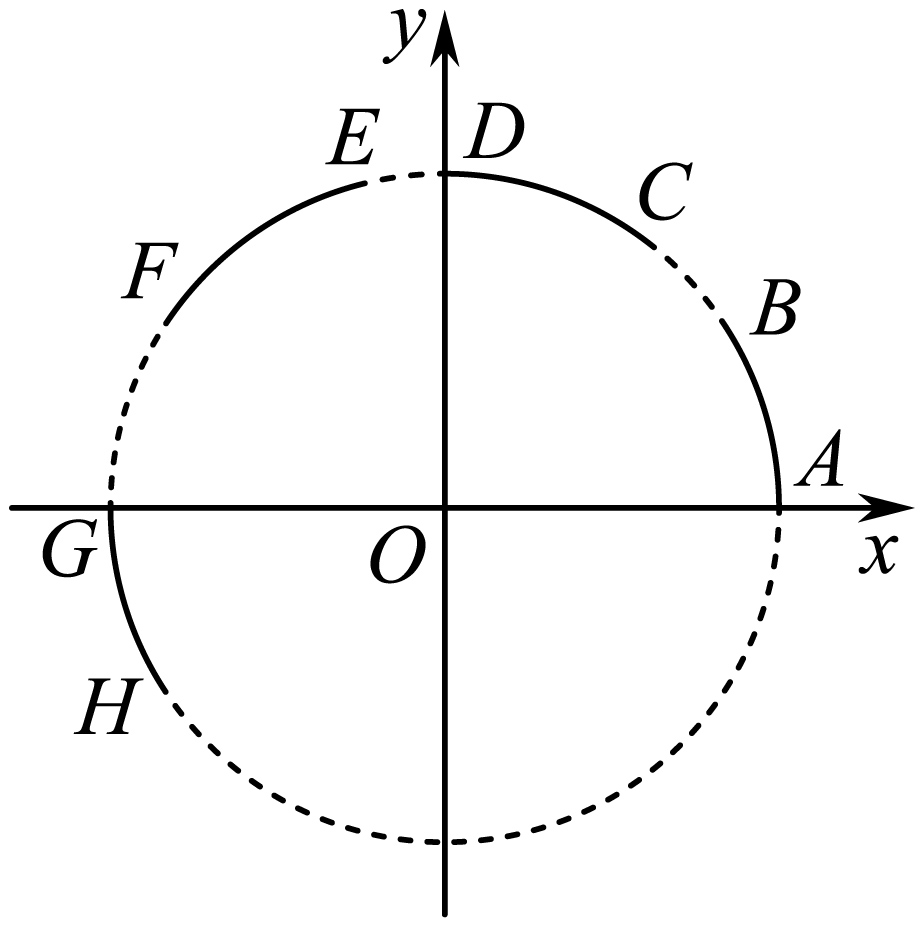
[2018 • 北京高考] 在平面直角坐标系中,
A. AB B. CD C. EF D. GH
解题思路
答案是 C。
3)诱导公式 - 锐角三角形小的二级结论
知识点
由
由于
结论:在锐角三角形中,一个角的
题目
题目一
已知
A.
B.
C.
D.
解题思路
A. 在三角形中,
,所以 。因此 ,此结论一定成立。 B. 因为
,所以 。因此 ,此结论一定成立。 D.
。因为锐角三角形小的二级结论,可以知道 ,因此 。同理, 。最后, 。
答案是 A, B, D。
4)大胆画三角函数图像
题目
已知函数
A.
B.
C.
D.
解题思路
答案是 A, B, D。
5. 函数图像变换
1)基础题型
题目一
[2022 • 浙江高考] 为了得到函数
A. 向左平移
B. 向右平移
C. 向左平移
D. 向右平移
解题思路
答案是 D。
题目二
已知曲线
A. 把
B. 把
C. 把
D. 把
解题思路
答案是 D。
题目三
把函数
A.
B.
C.
D.
解题思路
答案是 B。
2)整体代换
“整体法”研究
比如:
首先,令
对称轴
对称中心 / 零点
单调增区间
题目一
[2020 • 江苏高考] 将函数
解题思路
根据题意,平移后的函数为:
令
由
问与
当
当
题目二
[2023 • 广州中山大学附中高三期中] 已知函数
解题思路
首先计算周期 ( T ):
由
当 (k = 0) 时:
当 (k = 1) 时:
当 (k = 2) 时:
题目三
[2022 • 全国甲卷] 将函数
A.
解题思路
【分析】先根据平移变换得到曲线
【详解】由题意知,曲线
又
故选:C
题目四
[2018 • 北京高考] 设函数
解题思路
【分析】根据题意
【详解】因为
【点睛】函数
; - 周期
; - 由
求对称轴,最大值对应自变量满足 ,最小值对应自变量满足 ; - 由
求增区间;由 求减区间。
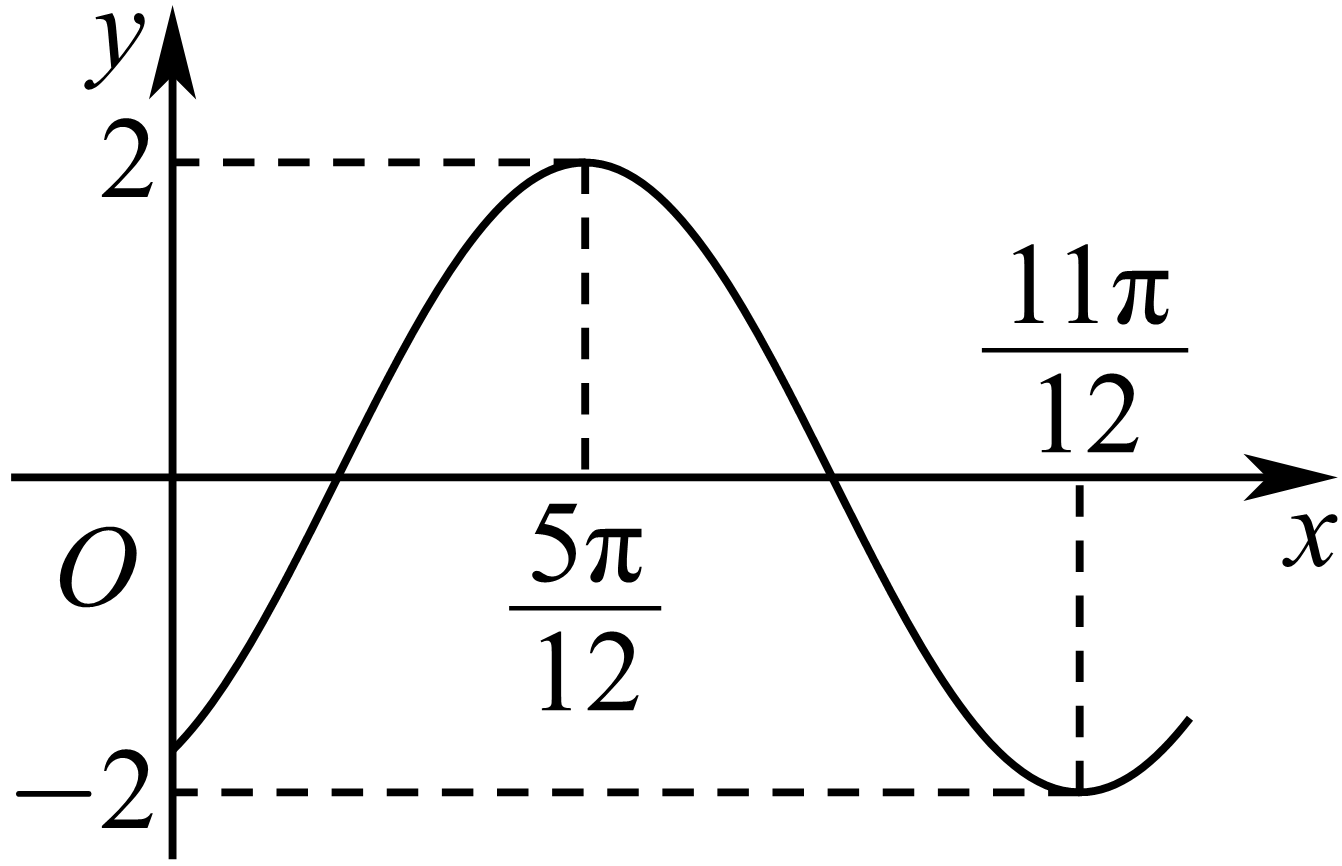
题目五
函数
A. (2,
解题思路
【分析】根据图像最高点与相邻最低点的横坐标标示,求出周期,进而求出
【详解】根据图像可得周期
再由最高点的横坐标为
故选:D
题目六
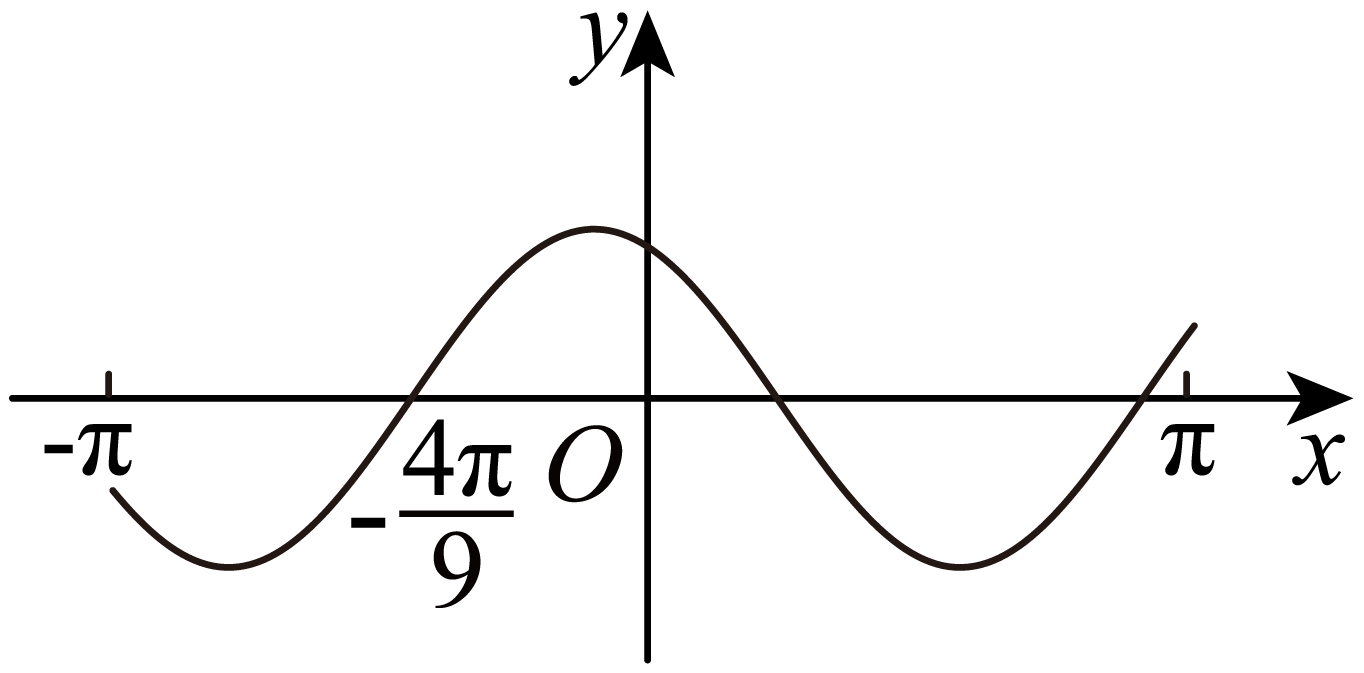
[2022 • 新课标一卷] 设函数
A.
解题思路
【分析】将
【详解】由图像可得
所以
设函数
所以
当
故选:C
“整体法”+“找对应点”还能做性质判断 ! !
题目一
已知函数
A.
B.
C.
D.
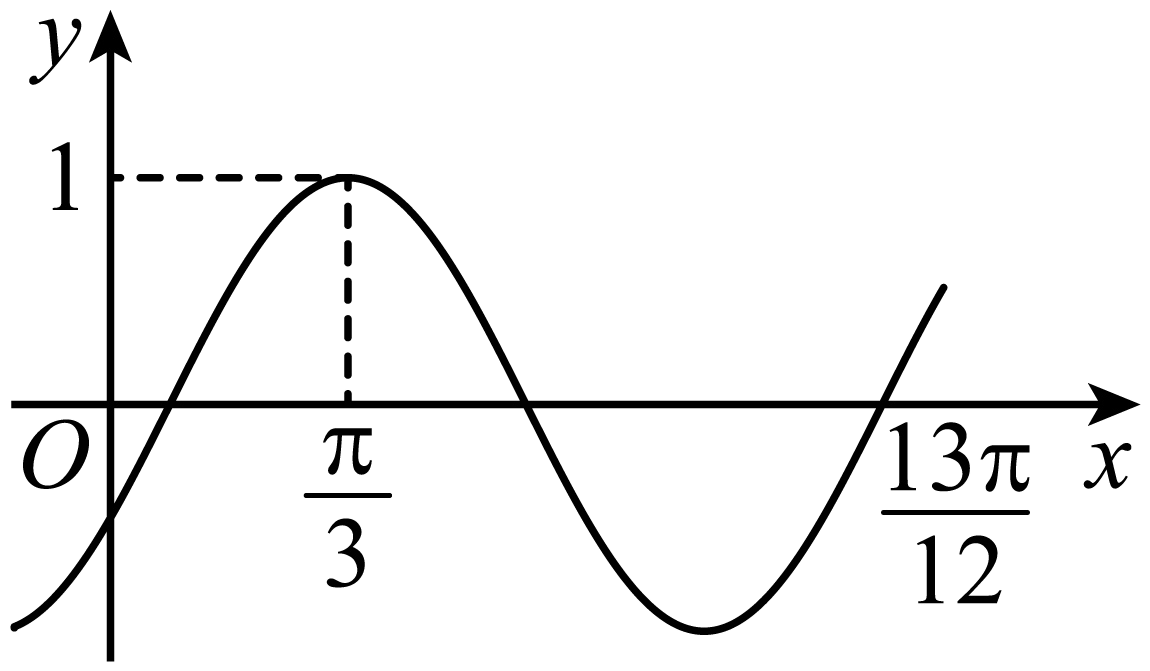
三角恒等变换
1. 简单应用
题目一
A.
解题思路
要解决这个问题,我们需要利用三角函数的和差公式。具体来说,题目中的表达式可以通过余弦差角公式来简化:
根据余弦差角公式,我们有:
在这里,令
我们知道:
因此,答案是:
所以,正确答案是选项 A。
题目二
解题思路
我们需要简化以下三角表达式:
步骤 1:使用三角恒等式
回顾正弦的和差公式:
注意到题目中的表达式类似于:
步骤 2:简化
首先,我们将
因此,表达式变为:
步骤 3:应用正弦和角公式
将简化后的表达式应用正弦和角公式:
步骤 4:计算
题目三
已知
A.
解题思路
即
得
即
得
故选:B
题目四
若
解题思路
回顾正切的和角公式:
将题目中的角度代入公式:
因此:
之后代入
题目五
已知
A.
解题思路
步骤 1:使用正切的和角公式
回顾正切的和角公式:
将题目中的角度代入公式:
因此:
已知
步骤 2:代入已知值
将
步骤 3:解方程
设
将方程两边乘以
化简得到:
再整理:
化简得到:
解这个一元二次方程:
所以:
题目六
如果
解题思路
步骤 1:求方程的根
方程
其中,
因此,方程的两根为:
步骤 2:使用正切的和角公式
回顾正切的和角公式:
将
因此:
2. 进阶应用 - 找角关系&巧用
题目一
计算
A.
解题思路
由
题目二
已知
A.
解题思路
分析 根据同角三角函数的基本关系求出
详解 因为
所以
所以
故选:D
题目三
在
A.
解题思路
因为
因为
所以
题目四
已知
A.
思路一
步骤 1:使用
回顾
我们知道:
因此:
步骤 2:代入已知值
已知:
将其代入公式:
将分子分母同时乘以
步骤 3:化简表达式
我们需要计算:
将分子分母同时乘以
化简得到:
思路二【推荐】
可以使用
步骤 1:使用
回顾
将题目中的角度代入公式:
因此:
步骤 2:计算角度差
计算
因此:
步骤 3:化简
已知
已知
题目五
已知
A.
解题思路
步骤 1:使用正切函数的和角公式
回顾正切函数的和角公式:
我们设
已知
步骤 2:化简表达式
将上述公式变形得到:
整理得:
移项得到:
3. 综合应用
1)直接用
题目一
已知
A.
解题思路
故选:C
题目二
若
A.
解题思路
答案选 C。
2)先变形,再用公式
题目一
已知
A.
解题思路
题目二
已知
解题思路
两边平方可得:
两边平方可得:
由
故答案为:
3)找角关系
题目一
若
A.
解题思路
思路
先由
转化
详细
由题意
故
又
故
则
故选:C