必修一数学 - 知识点
第五章:三角函数
一、任意角和弧度制
1. 任意角
(1)角的概念
角可以看成平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形。

射线的端点叫做角的顶点,射线在起始位置和终止位置分别叫做角的始边和终边。
(2)角的分类
旋转方向
按逆时针方向旋转所成的角叫正角;
按顺时针方向旋转所成的角叫负角;
一条射线没有作任何旋转而形成的角叫零角。
这样,我们就把角的概念推广到了任意角。
终边位置
象限角
概念
当角的顶点与坐标原点重合,角的始边与轴的非负半轴重合,那么角的终边(除端点外)在第几象限,就说这个角是第几象限角。如果角的终边落在坐标轴上,这时这个角不属于任何象限。
终边相同的角
所有与角
- 即任一与角
终边相同的角,都可以表示成角 与整数个周角的和。 - 终边相同的角不一定相等,但相等的角,终边一定相同。
- 终边相同的角有无数多个,它们相差
的整数倍。
象限角的表示
| 象限角 | 集合表示 |
|---|---|
| 第一象限的集合 | |
| 第二象限角的集合 | |
| 第三象限角的集合 | |
| 第四象限角的集合 |
轴线角
| 位置 | 表示 |
|---|---|
| 终边在 x 轴非负半轴 | |
| 终边在 x 轴非正半轴 | |
| 终边在 x 轴 | |
| 终边在 y 轴非负半轴 | |
| 终边在 y 轴非正半轴 | |
| 终边在 y 轴 | |
| 终边在坐标轴 |
2. 弧度制
(1)弧度的概念
定义
以弧度为单位度量角的单位制叫做弧度制。
度量方法
长度等于半径长的圆弧所对的圆心角叫做 1 弧度的角。下图

弧度数
如果半径为
正角的弧度数是一个正数,负角的弧度数是一个负数,零角的弧度数是 0。
记法
弧度单位用符号 rad 表示,或用“弧度”两个字表示。在用弧度制表示角时,单位通常省略不写。
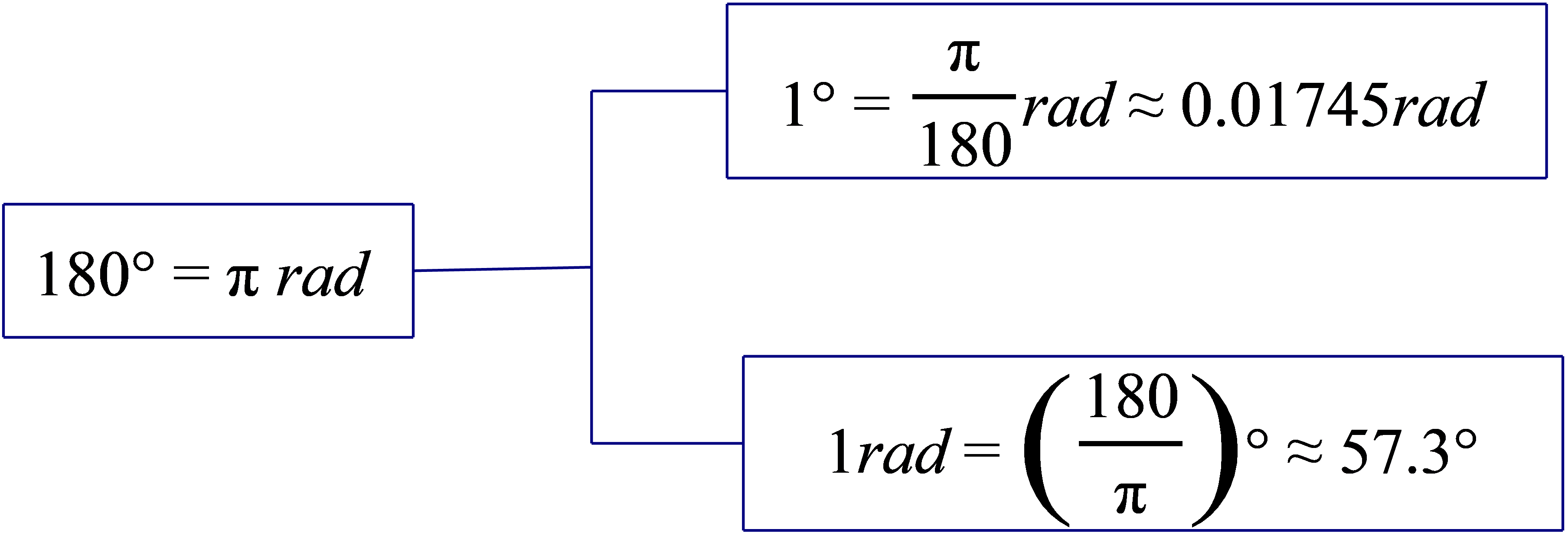
(2)弧度与角度的换算
如果是角度换弧度,就角度乘以
如果是弧度换角度,就把
常见角度的弧度制
| 0° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° | 270° | 360° |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 |
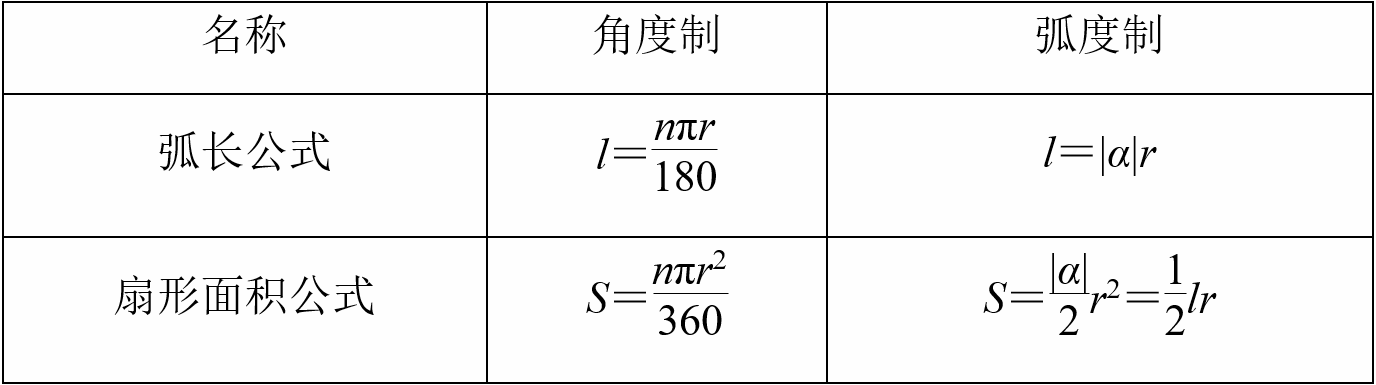
(3)关于扇形的几个公式
证明方法
对应成比例
设扇形的圆心角为
角度制下的公式 弧度制下的公式
由圆心角为
角度制公式 ==> 弧度制公式
二、任意角的三角函数
1. 三角函数的概念
(1)三角函数的定义
一般地,任意给定一个
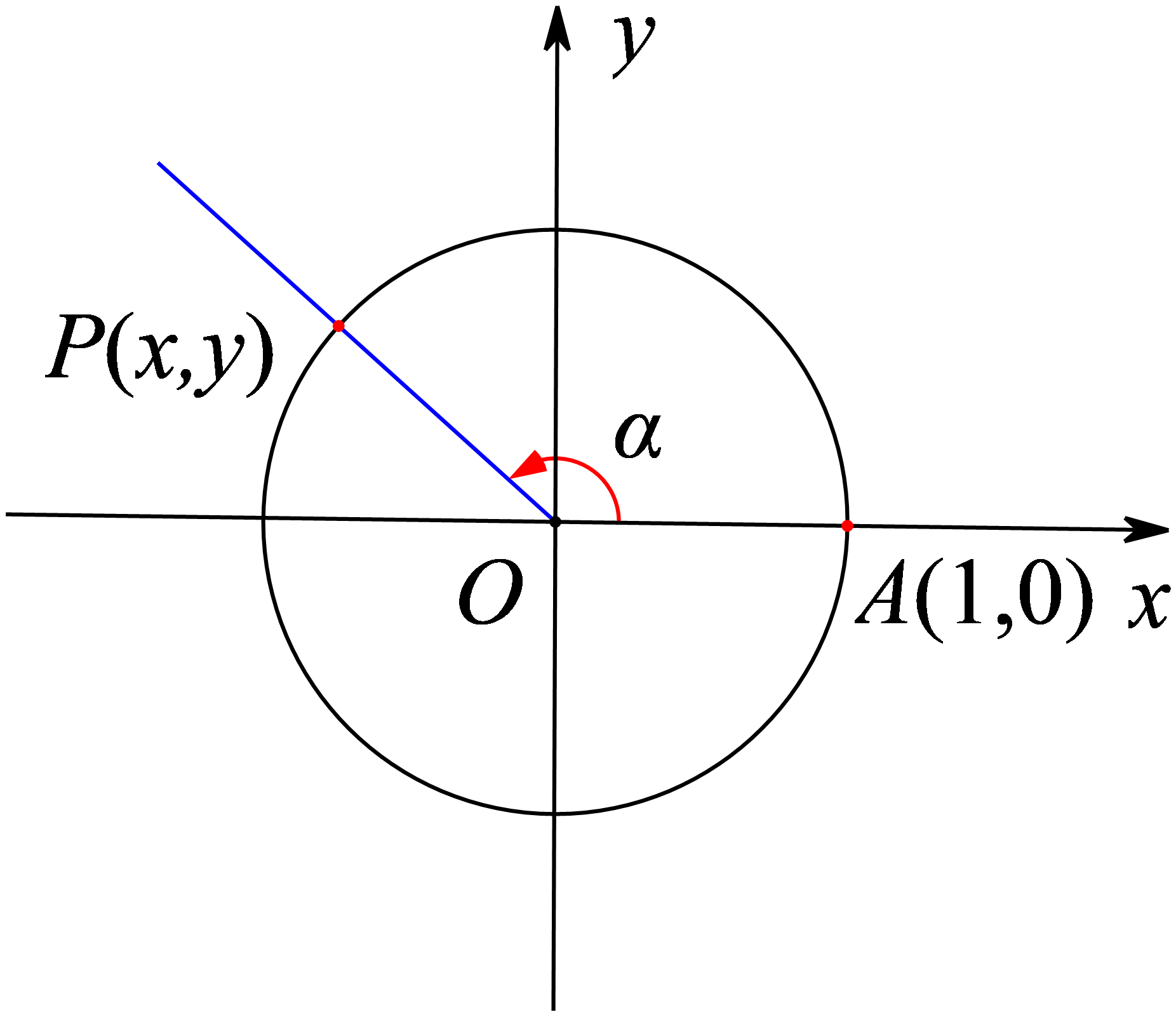
把点 正弦函数,记作 $ \sin \alpha $,即
把点 余弦函数,记作
把点
正弦函数、余弦函数和正切函数统称为三角函数,通常将它们记为:
正弦函数
余弦函数
正切函数
(2)几个特殊角的三角函数值
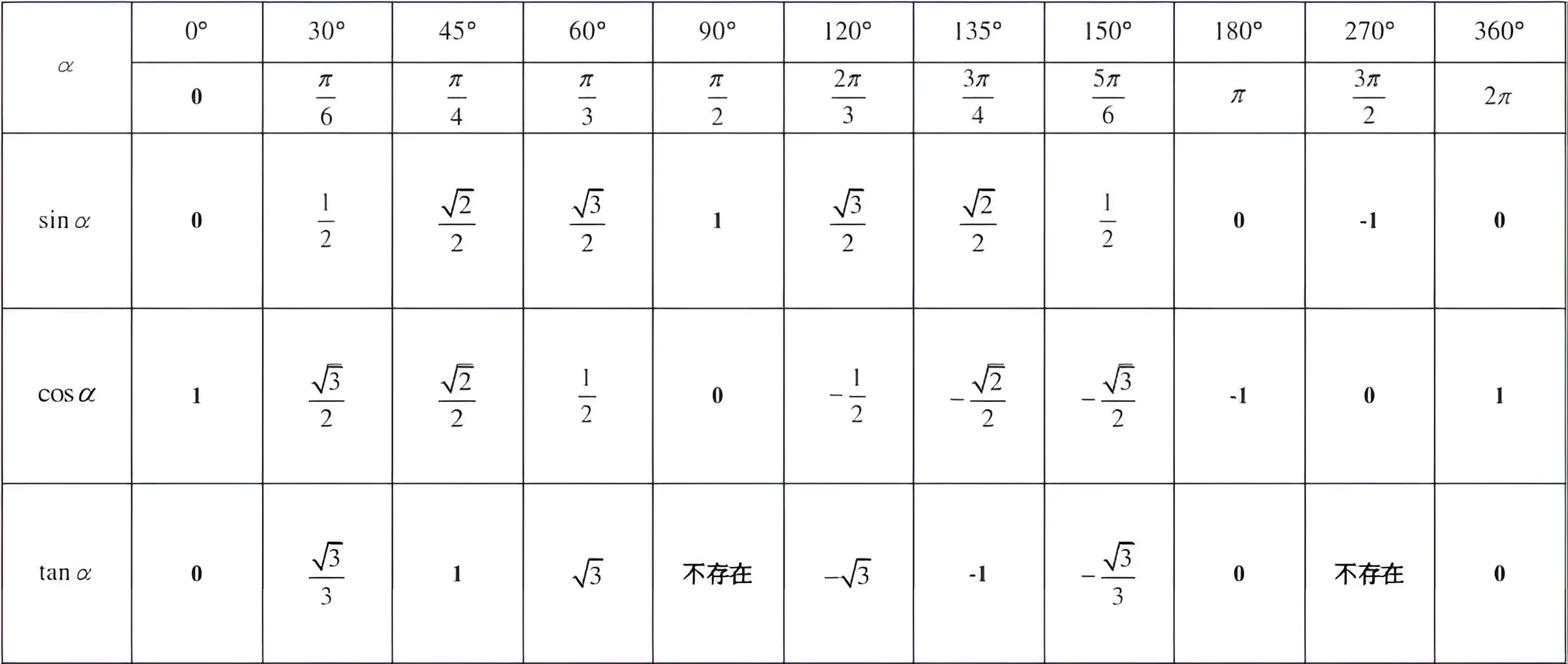
三角函数值补充
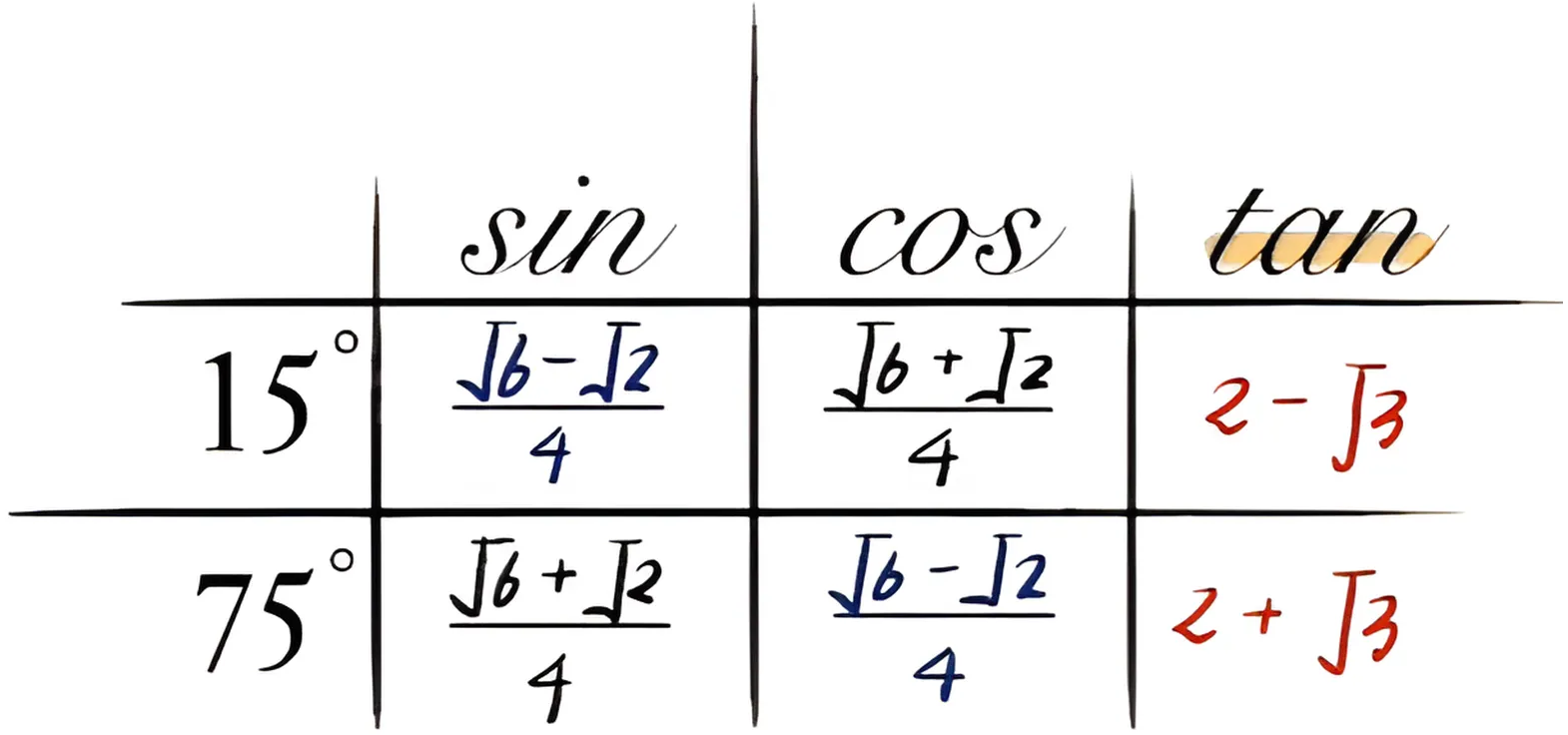
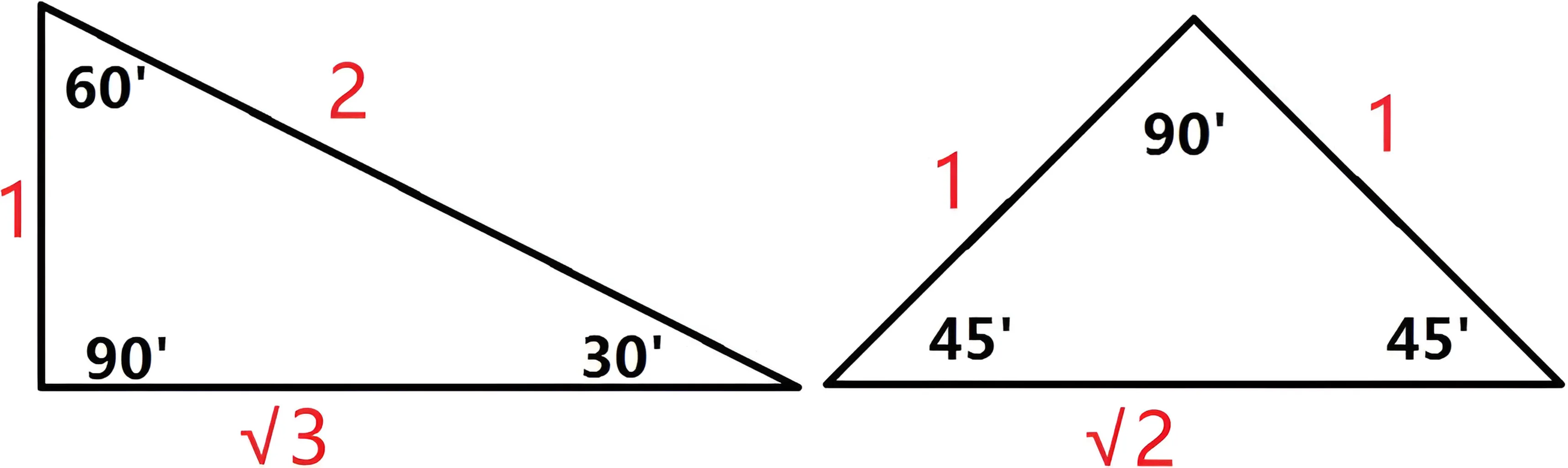
初中比较重要的特殊三角形
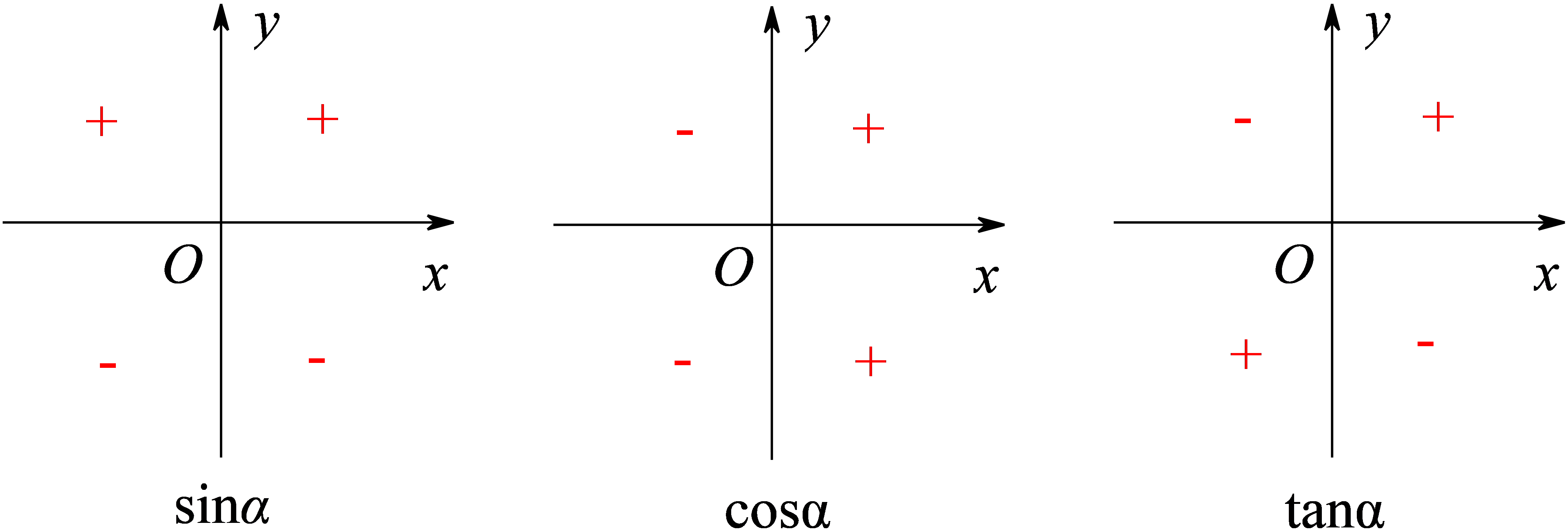
(3)三角函数值的符号
口诀记忆:“一全正,二正弦,三正切,四余弦”。
(4)同角三角函数间的基本关系
平方关系:
商数关系:
作用
① 已知
② 化简三角函数式。
③ 证明三角函数恒等式。
常用的等价变形
变形公式的应用要注意哪些方面?
使用变形公式
, 时,“ ”号是由 的终边所在的象限确定的,而对于其他形式的变形公式就不必考虑符号问题。 对这些关系式不仅要牢牢掌握,还要能灵活运用(正用、逆用、变形应用)。
2. 诱导公式
第一组:
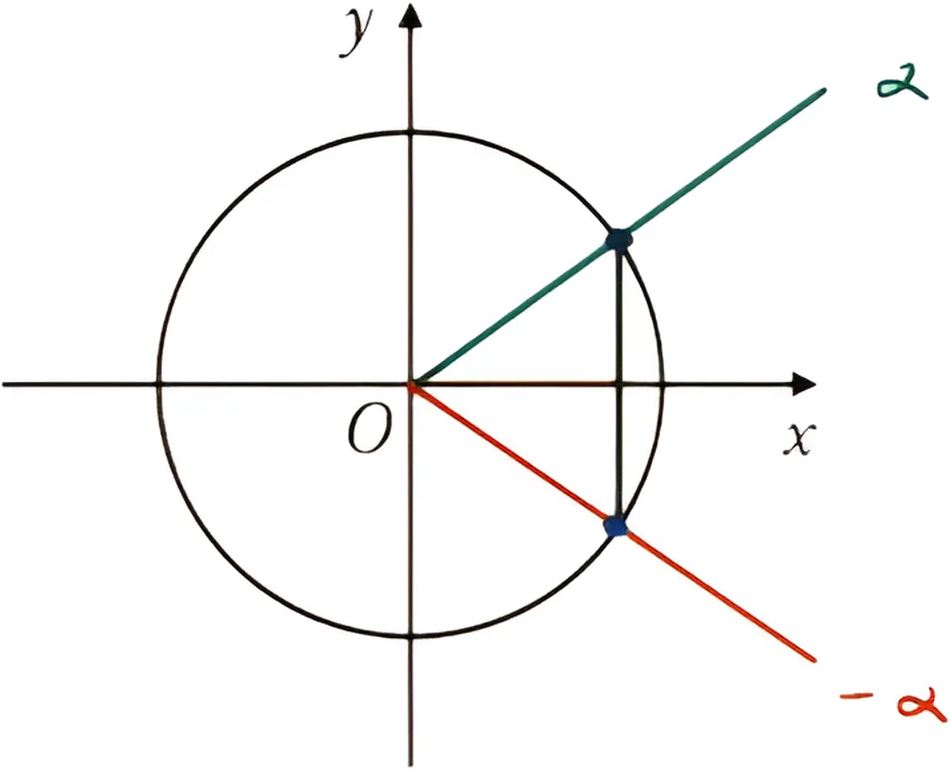
第二组
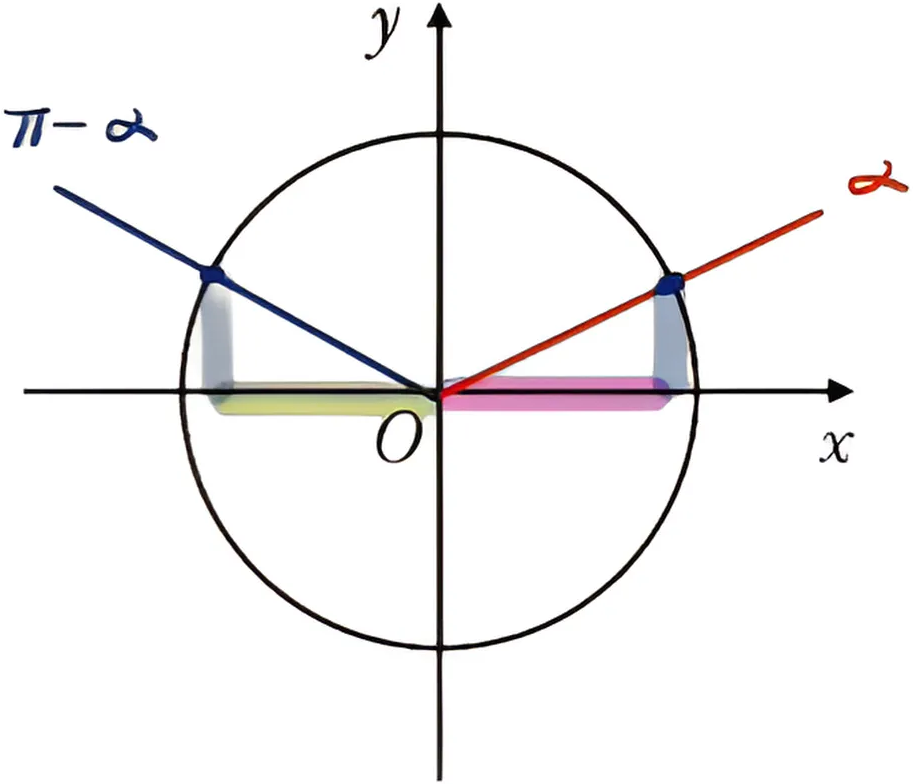
第三组
注:
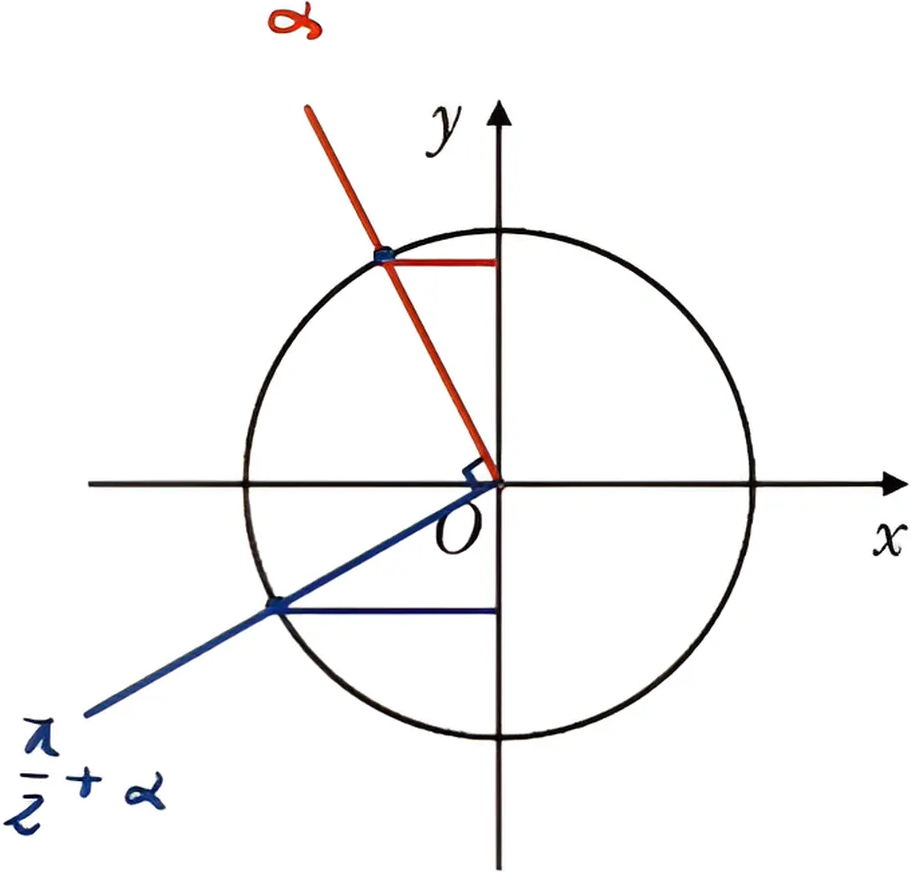
第二组与第三组公式记忆口诀:奇变偶不变,符号看象限。
3. 三角函数的图像、性质与变换
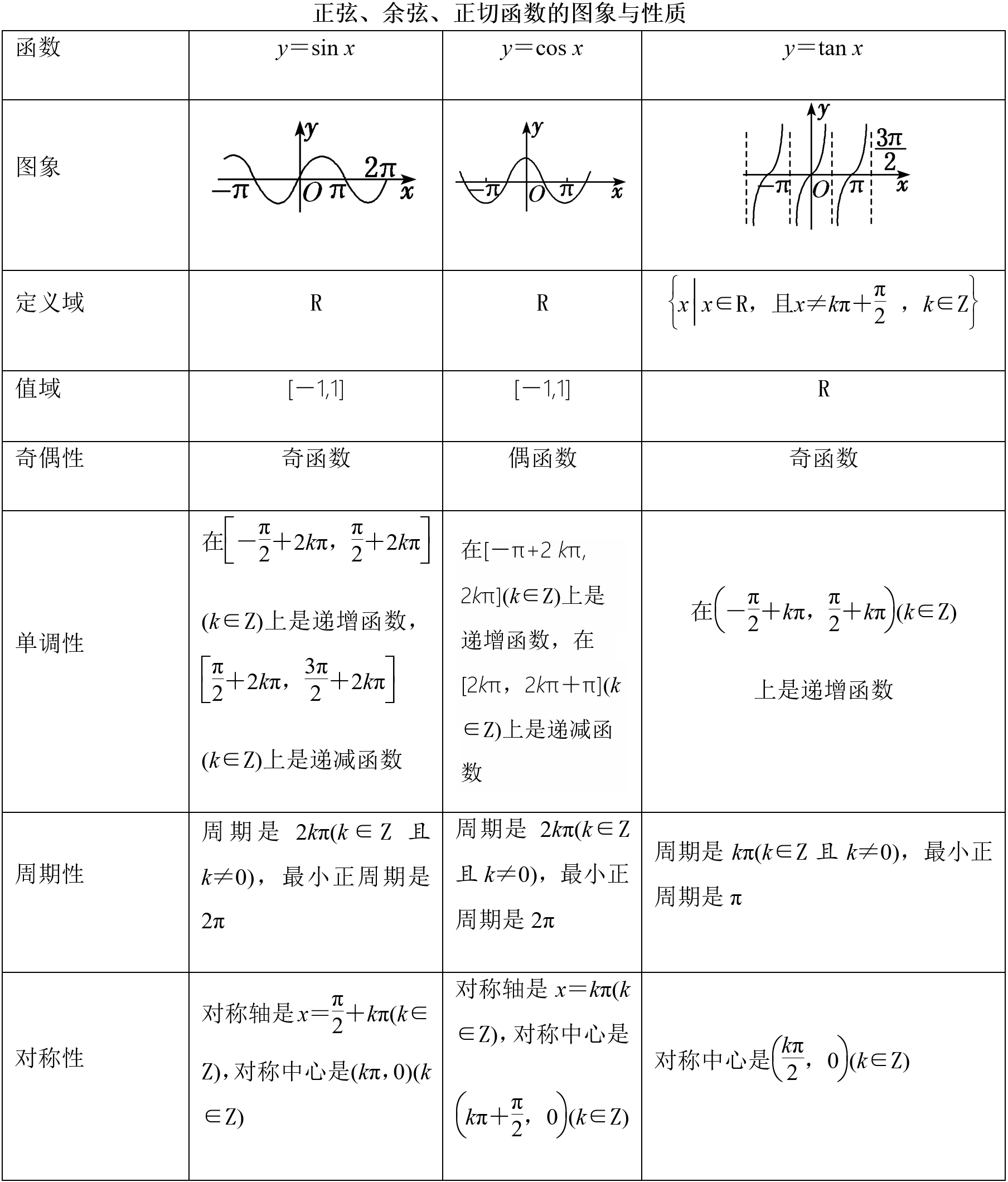
1)图像
(1)正弦函数的图象
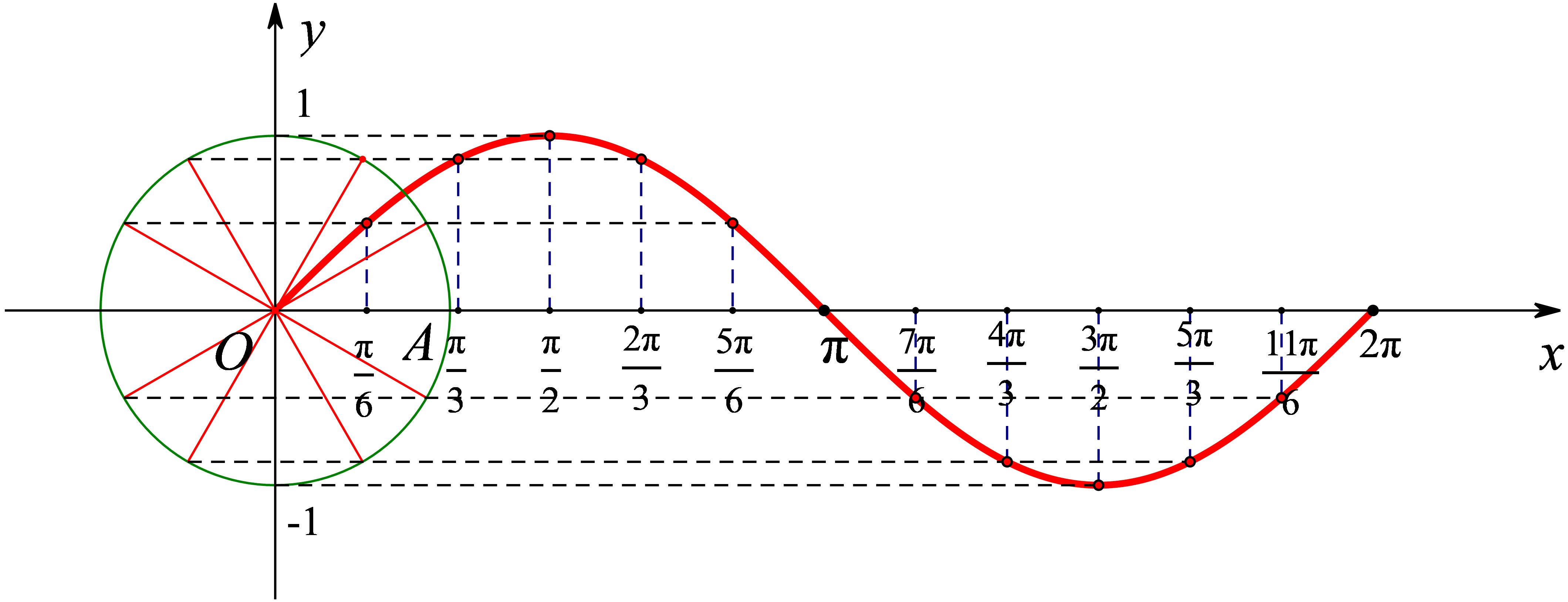

(2)余弦函数的图象
因为

(3)正切函数的图象
设
由此可见,当
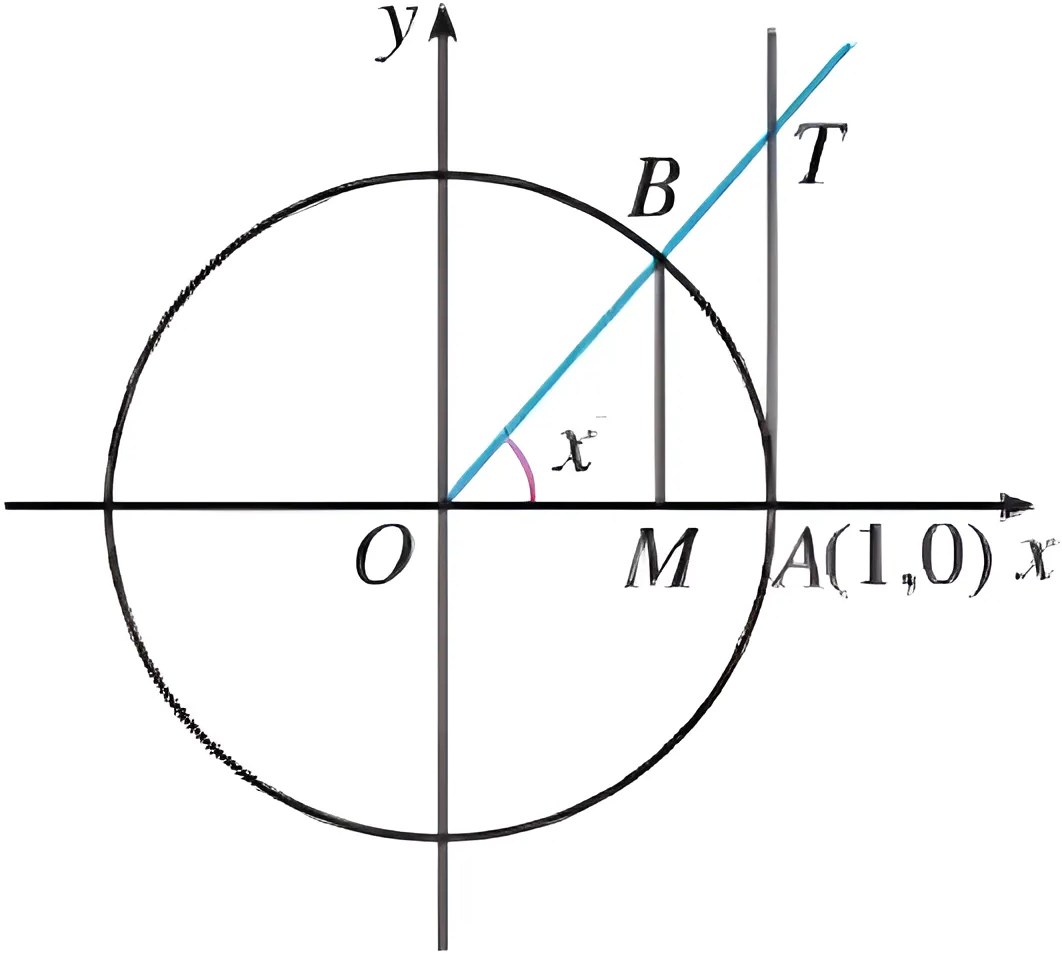
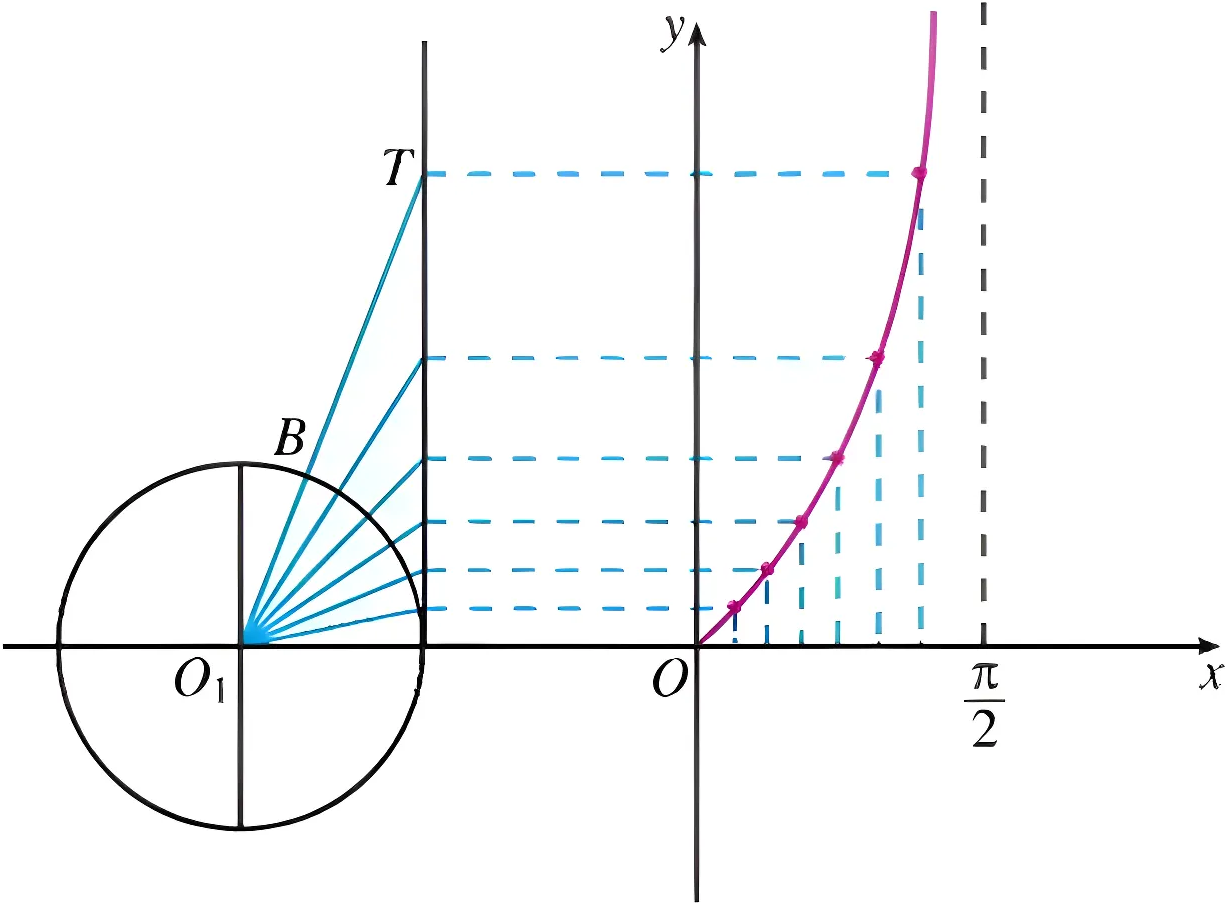
最后得到正切函数的图象。
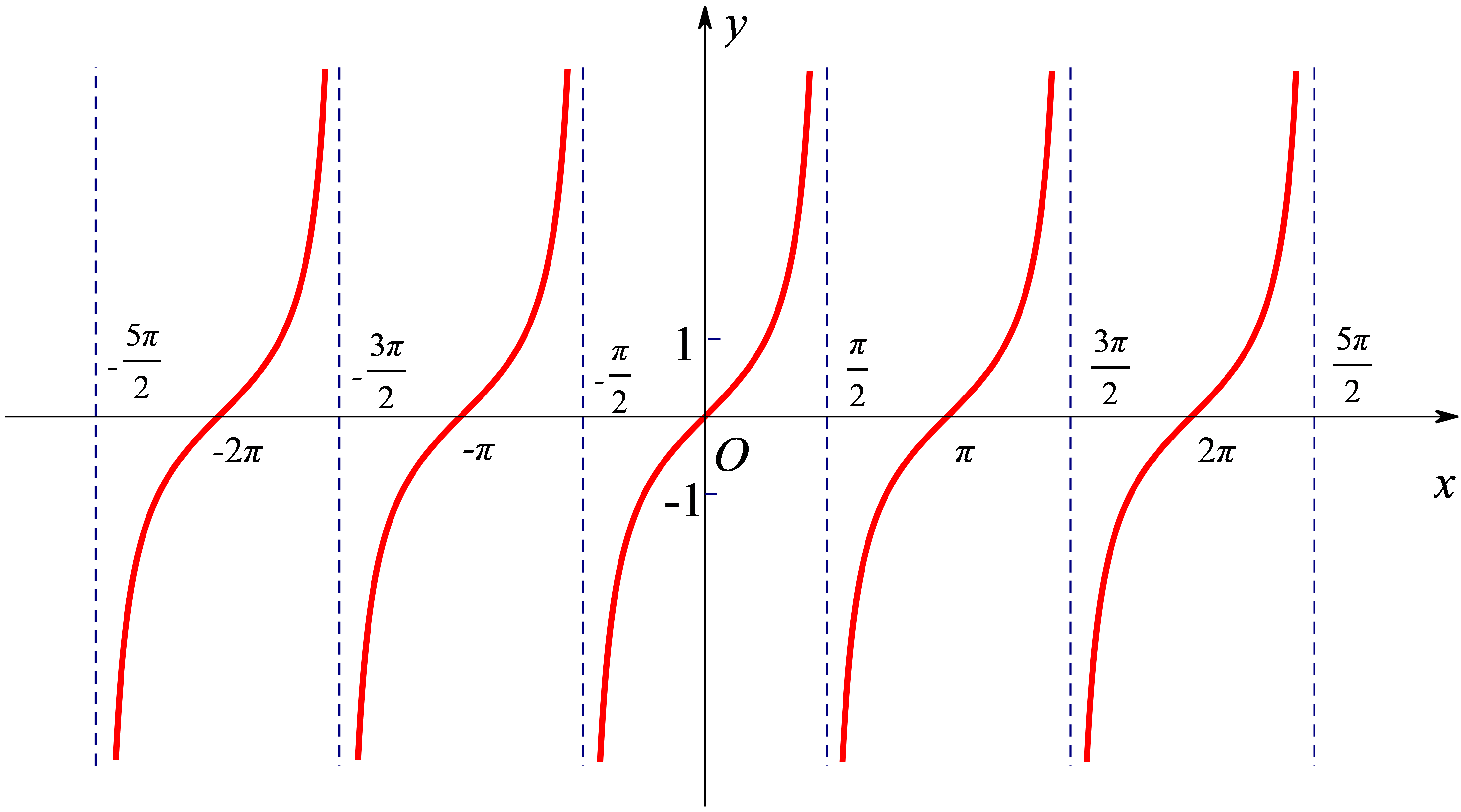
2)函数图像变换
初中我们就学习过函数平移转换口诀:左加右减,自变量;上加下减,因变量。那函数伸缩是什么?
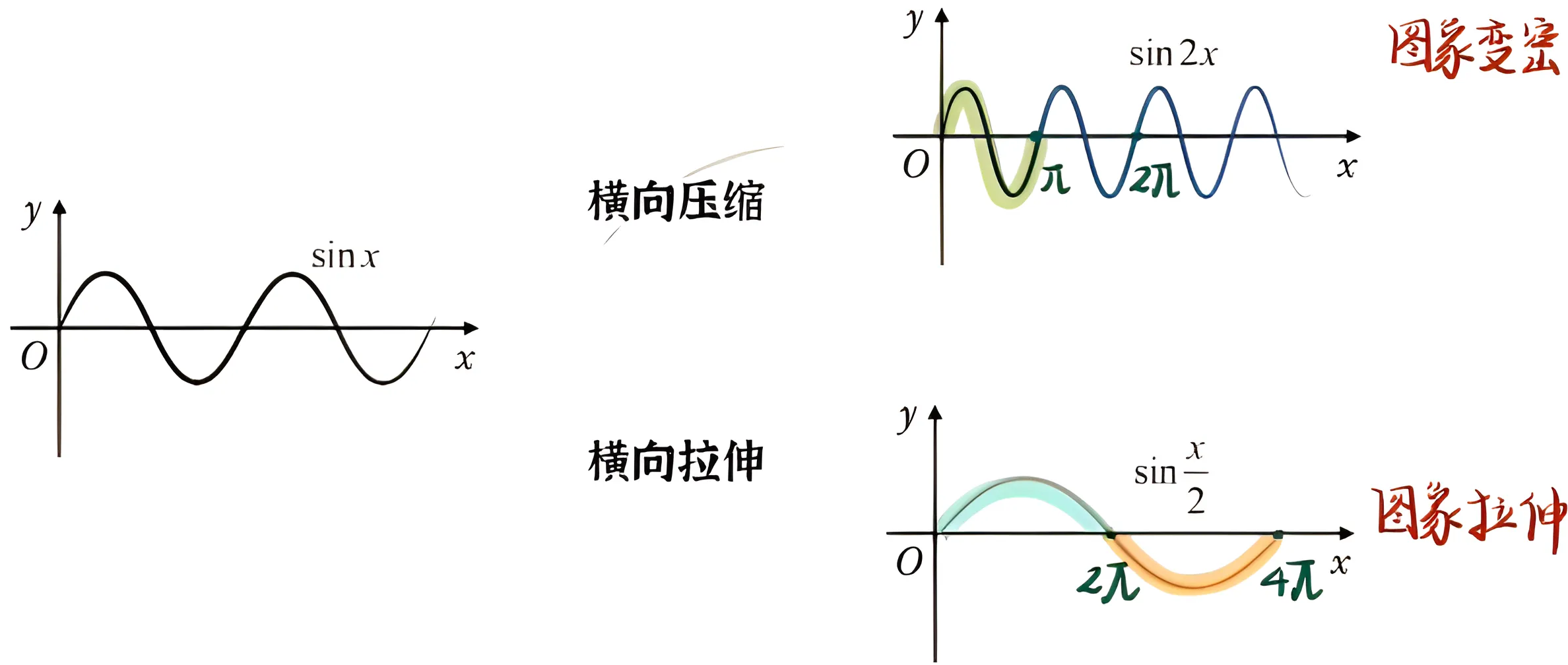
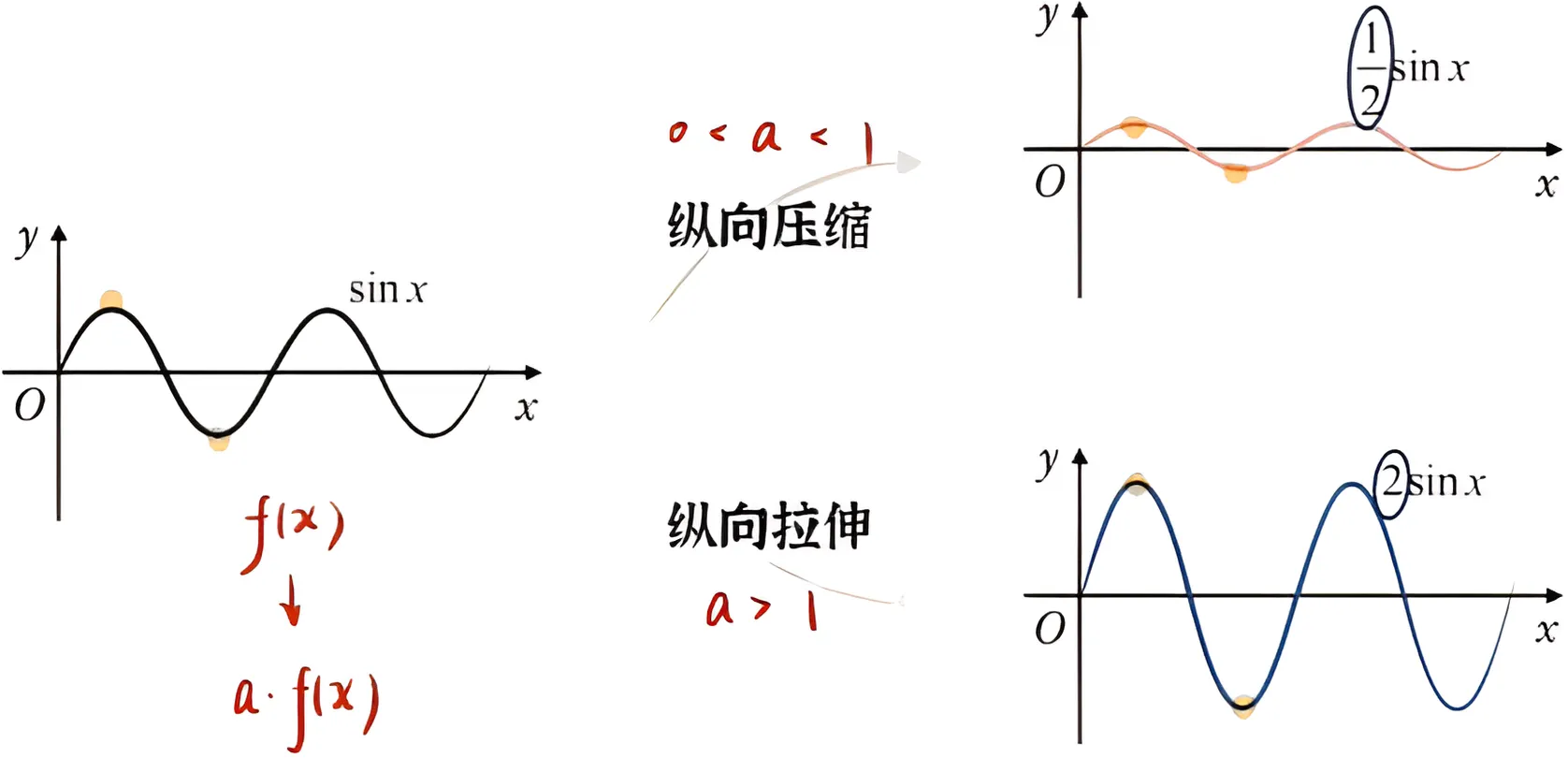
由
先平移后伸缩
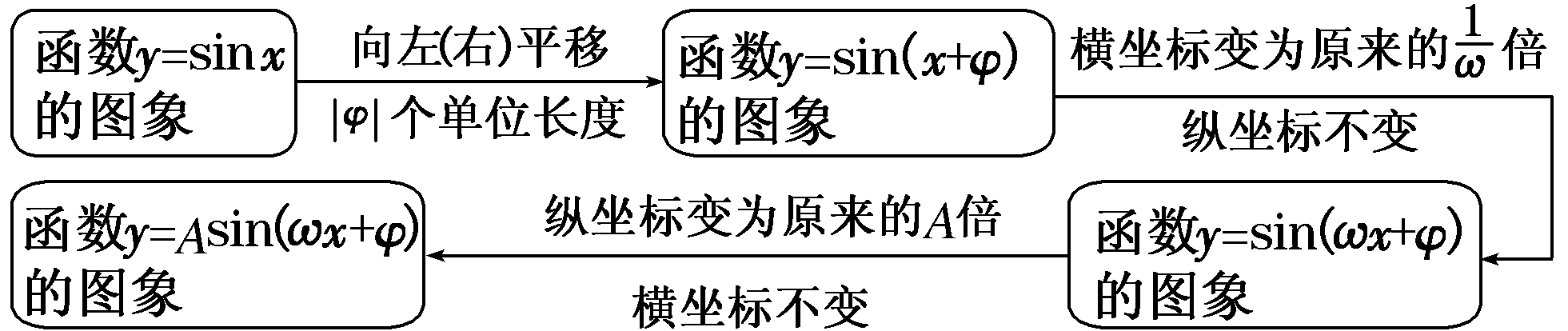
先伸缩后平移
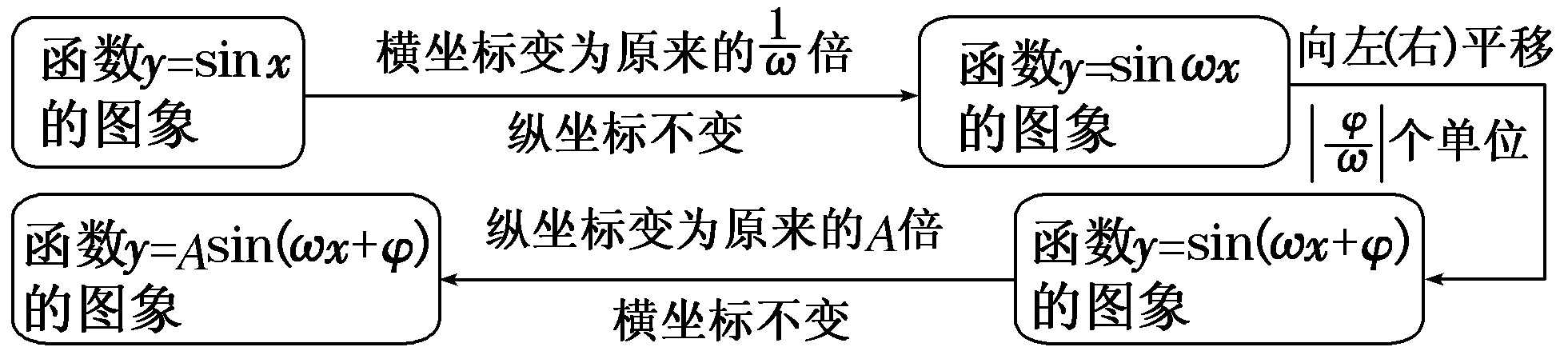
函数
物理中,描述简谐运动的物理量,如振幅、周期和频率等都与函数
| 振幅 | 周期 | 频率 | 相位 | 初相 | |
|---|---|---|---|---|---|
4. 三角恒等变换
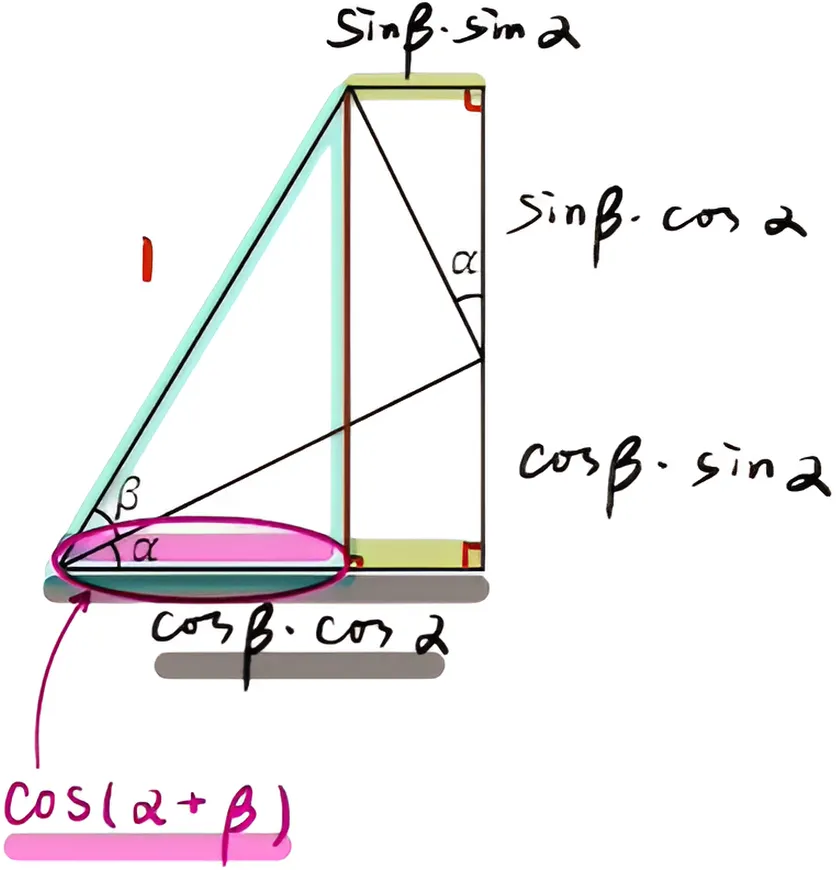
(1)和角公式
(2)差角公式